コズミックサーフィンでは、恒星の固有運動を、宇宙空間における等速直線運動と仮定 しました。最も単純化された仮定ではありますが、この運動を記述するためには、狭義の 固有運動（赤経方向と赤緯方向の２値）の他、視線速度と距離のデータが必要となります。 これらのデータは全て、Yale Brught Star Catalogue（BSC）のものを採用しています。 ただし、距離については年周視差から換算します。 この方法に寄れば、恒星までの距離の変化も算出されますので、光度の変化も表現されます。
　さて、いきなりここで重要な近似が発生します。BSC データは各種星表の中でも項目,星数 ともに充実しているものですが、それでも視線速度と年周視差については記述の無い恒星も 数多く含まれています。（年周視差においては値が負のものもあります。これは原理的には 有り得ませんので測定誤差によるものと考えられます。）このような恒星については、視線 速度は「+/-0」，年周視差は「 0.0001″」として近似してあります。年周視差を「 0″」 としてしまうと同じ方法では計算が出来なくなるためです。しかし、このように近似しても、 時間の変化に対する計算上の誤差は微量であり無視できます。

　恒星の空間的な移動を再現するために、以下の５種類のデータが必要となります。

  ａ．現在の恒星の位置
          AD2000年分点のデータ。赤経α0と赤緯δ0で示す。
  ｂ．現在の恒星の光度：Visual Magnitude
        視光度。Vで示す。単位は（等）。
  ｃ．固有運動：Proper Motion
        年間の運動量を赤経方向の成分μαと赤緯方向の成分μδで示す。
        なお、μαは極座標の性質から、極に近づくほど計測上の値が拡大
        されてしまうので、cosδを乗じて、実質的な運動量に修正されて
        いる。
  ｄ．年周視差：Parallax
        地球の公転により、１年周期で恒星の視位置が天球上を楕円を描い
        て運動するように見える。この運動を年周視差という。年周視差は
        極めて微量であるが、原理上、近距離にある恒星ほど大きな量とし
        て観測される。
        年周視差をΠ（単位：″）とすると、恒星までの距離ｄ（光年）は、
                ｄ＝３．２６２／Π
        となる。
  ｅ．視線速度：Radial Velocity
        恒星の空間運動の視線方向の成分。Ｒで示す。単位は（km/s）。
        視線速度Ｒは分光観測により、恒星の光のドップラー効果を測定し
        て求められる。

以上のデータから固有運動による視位置の変化を推算します。下図において、 １年間の固有運動μα,μδから、１年後の恒星の位置Ｘ' は実質的な移動量μ と位置角φで表わせます。μα,μδ,μ,φ の関係を式にすると、
　　　μα＝μ sinφ ･････････････(1)
　　　μδ＝μ cosφ ･････････････(2)
この(1)(2)式から、μ と φ を求めることが出来ます。

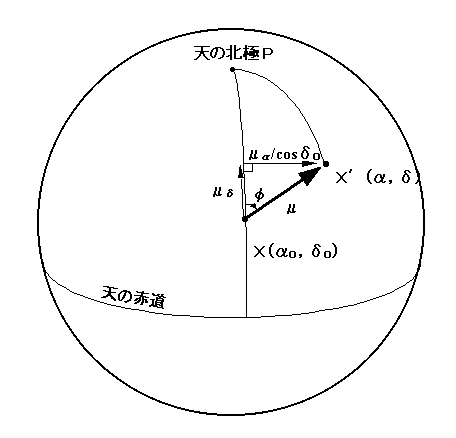
天球上の１年間の固有運動

赤経方向の固有運動μαは、赤緯δによらない数値であるので、 球面座標上の赤経の移動量を求めるために、cosδ0で除する。

　つぎに、下図から過去や将来の恒星の位置を推算します。 図は、恒星の空間運動を、固有運動μ、視線速度Ｒ、距離ｄ で表したものです。 Ｓ点は太陽の位置、恒星の空間上の現在の位置をＡ、移動後の位置をＢとします。 Ａ' は１年後の位置です。また、ｎは１年間の秒数、ｌ は移動後の角距離です。

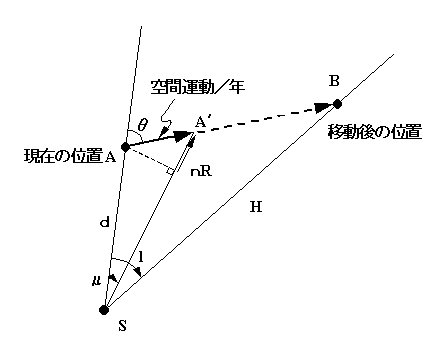
恒星の空間運動

　すでに分かっている、μ，ｄ，Ｒ から、θ，AA' を算出します。これを直線的に延長して、 任意の時代の恒星の移動位置 Ｂ をθ，AB として求め、これから、角移動量 ｌ が算出されます。ここで、移動した後の太陽からの距離 Ｈ を算出しておきます。 あとは、天球上の固有運動の方向を φ として求められていますので、 最終的に移動後の赤経，赤緯 が計算されます。

　固有運動が空間運動である以上、恒星の光度の変化が発生します。 この効果は、移動後の光度を V' とすると、
　　　V'＝V＋５ log(Ｈ／ｄ)
で表されます。

BSC vs Hipparcos

　最近では精密な星表としてHipparcos CatalogueがBSCに代わって採用されるようになって きました。コズミックサーフィンでもHipparcosのデータを採用することを検討しましたが、 実際に調査してみると Hipparcos のデータは膨大すぎて、開発するに持て余すほどでした。 さらに、Hipparcosには、視線速度のデータが無いことが分かり、Hipparcos Input Catalogue（Hipparcos で観測するために，それまでに地上の観測から求められていたもの をまとめたもの）から引用してくる必要もありました。
　あれこれ検討を重ねた結果、「このソフトに要求される精度を考えると、BSC で十分」 と結論したのでした。しかしながら、開発者としては未練のあることも事実。特に、空間 旅行については、Hipparcos のもつ詳細なる年周視差（＝距離）のデータはたいへん魅力です。 もし、「次ぎ」があれば、Hipparcos Catalogue の採用は最初に検討することになるでしょう。

パソコンの処理能力

　コズミックサーフィンでは、極めて長大な時間と空間を扱います。 恒星の運動は大変小さいため、通常の天体暦なら、要求される精度に見合った近似式を 織り込んで、計算量を減らすことが普通です。
　しかし、「極めて長大な」となるとそうは行きません。コズミックサーフィンでは、 これらの計算には殆ど近似を用いずに、極めてまじめに計算しています。 また、恒星の数も BSC の全9,110星を対象にしましたので、尋常な計算量ではなく、 これをどうやって快適に扱えるソフトにするかが、プログラマにとって大きな課題でした。 そのための工夫の跡を紹介すると．．．。

■デフォルトでの表示は５．５等までとし、それより暗い６．５等までの恒星は 「微光星」のオプションスイッチとした。

■「時間旅行」や「空間旅行」のアニメーションは、表示速度をユーザー側で可変とした。

．．．など。それでも快適な動作のためには、近年のパソコンでないと辛いところで、 （うぬぼれを覚悟で申し上げるなら）コズミックサーフィンの誕生は、 まさに時期を得ていたと痛感しているところです。