歳差運動について、もっとも一般的に使われている表現は、日月歳差や惑星歳差など 種々の歳差要因を、ひとまとめにした「一般歳差」です。一般歳差の定数も、 年代や文献によってわずかに異なっていますが、コズミックサーフィンでは以下に示す、 IAU1976年の天文定数系の数値を採用しました。
- (1) 一般歳差ψ=50.290966″+0.0222″T(/年)
- ここでTは、J2000からの時間経過を100ユリウス年で表した量。
- (2) 黄道傾斜角ε=23.439291°
一般歳差による座標の推算は下図に示す球面三角法により算出します。 なお、この推算法は東亜天文学会長谷川一郎氏により提案されたものです。
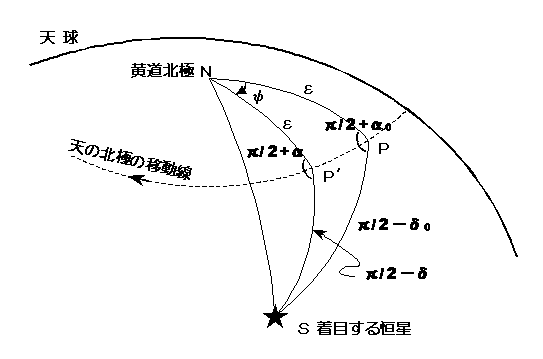
非常に長い期間の歳差運動
図中の記号は、
α0:基準年の恒星の赤経
δ0:基準年の恒星の赤緯
α :座標変換後の恒星の赤経
δ :座標変換後の恒星の赤緯
を示します。
△ PNX より、
cosd = cosε・sinδ0−sinε・cosδ0・sinα0
sind・sin(ψ+θ) = cosδ0・cosα0
sind・cos(ψ+θ) = sinε・sinδ0 + cosε・cosδ0・sinα0
△ NP'X より、
cosδ・cosα = sind・sinθ
cosδ・sinα = sind・cosε・cosθ−cosd・sinε
sinδ = cosd・cosε + sind・sinε・cosθ
以上から、α,δ を推算します。
2. J.H.Lieskeの歳差式について
かなり難解で、私には説明しきれません。コズミックサーフィンでも、
J.H.Lieske による推算式をそのまま使用しています。
ここらの解説は、
「天体の位置計算 増補版」長沢 工 著,地人書館(\2,000~)
に詳しいです。
 開発裏話
開発裏話
推算時間の限界歳差は、厳密には問題が複雑であり、長期間に渡り厳密に記述する理論は、今のところありません。 コズミックサーフィンでは、「長期間で安定」な式として「一般歳差」を、 「短期間で厳密」な式として「J.H.Lieskeの歳差式」を選択可能なように設計しましたが、 これは苦肉の策であったとも言えましょう。なお、一般歳差による記述でも、 約20万年を超えた過去に遡りますと、歳差が停止してしまうというおかしなことになります。 コズミックサーフィンの計算の限度は、過去と未来20万年までとしましたが、 このことが理由の一つであります。
−戻る−