■「経緯台の2点アラインメント」の計算方法
この項は、全面的に相馬充(国立天文台)氏の執筆によるものです。

2つの恒星S1, S2 の赤経・赤緯をそれぞれ(α1, δ1), (α2, δ2) とし,その望遠鏡目
盛環による方位角・高度の(誤差を持ったままの)読みをそれぞれ(A1, a1), (A2, a2)
とする.ここで方位角は右まわりに測るものとする(たとえば,北から東まわりに,という
ように測るのですが,方位角のゼロ点は特に北に合っているわけではないので,単に「右まわり」
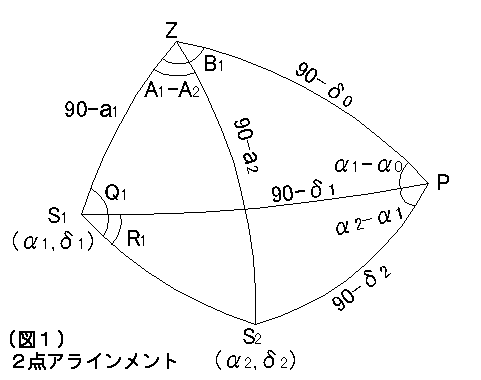
と言っているのです).図1でP は天の北極,Z は望遠鏡の天頂である.
図1で∠PS1S2 = R1, ∠ZS1S2 = Q1, S1S2 = D (0°≦D≦180°) とおくと
sinDsinR1 = cos δ2 sin(α2 - α1) (1)
sinDcosR1 = sin δ2 cos δ1 - cos δ2 sin δ1 cos(α2 - α1) (2)
より,R1 が求められる(sinD≧ 0 より,(1) と(2) の符号がそれぞれsinR1 と cosR1
の符号に等しいことからR1 の象限が決まり,tanR1 = (1)/(2) よりR1 が求められる.
この種の方程式の解き方は,以下,同じである).また
sinDsinQ1 = cos a2 sin(A1 - A2) (3)
sinDcosQ1 = sin a2 cos a1 - cos a2 sin a1 cos(A1 - A2) (4)
より,Q1 も求められる.
注:D をたとえばcosD = sin δ2 sin δ1 +cos δ2 cos δ1 cos(α2 -α1) から求めると,
Q1 はcosQ1 = (sin a2 - cosDsin a1)= sinDcos a1 を使って求められるという
考え方もあるでしょうが,これだけではQ1 の象限までは決められないので,これは検算
に用いる程度にとどめるべきでしょう.
次に,望遠鏡の天頂Z の赤経・赤緯(α0, δ0) を
cos δ0 sin(α1 - α0) = cos a1 sin(Q1 - R1) (5)
cos δ0 cos(α1 - α0) = sin a1 cos δ1 - cos a1 sin δ1 cos(Q1 - R1) (6)
sin δ0 = sin a1 sin δ1 + cos a1 cos δ1 cos(Q1 - R1) (7)
により求める(α0 は(5) と(6) から,δ0 は(7) から).また,∠PZS2 = B1 を
cos δ0 sinB1 = cos δ1 sin(Q1 - R1) (8)
cos δ0 cosB1 = sin δ1 cos a1 - cos δ1 sin a1 cos(Q1 - R1) (9)
により求める.
A0 = A1 - B1 (10)
から求められるA0 が天の北極P の望遠鏡の目盛環による方位角の読みになる.
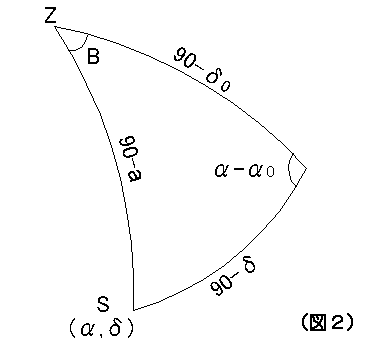
図2で,導入したい星S の赤経・赤緯を(α, δ) とし,その望遠鏡の天頂を基準に
した高度を a(-90°≦a≦+90°), 方位角に当たる∠PZS をB とおくと
cos a sinB = cos δ sin(α - α0) (11)
cos a cosB = sin δ cos δ0 - cos δ sin δ0 cos(α - α0) (12)
sin a = sin δ sin δ0 + cos δ cos δ0 cos(α - α0) (13)
が成り立つ.これによりa とB を求め,
A = A0 + B (14)
とすれば,望遠鏡の目盛環により高度と方位角をそれぞれa とA に合わせれば,目
的の星が導入できる.
この解法によると、水平の合っていない経緯台でもアラインメント可能です。
しかし、プラネタリウムソフト側は、ソフト上で設定された方位と高度で導入のパルス数を
与えますので、やはり設置はできるだけ正確に行うべきです。
また、上記のアラインメント方法では、1番目と2番目の恒星のアライメント間の時刻を無視
していますので、その間の日周運動は誤差になります。市販の経緯台式自動導入架台の多く
では、3点以上のアラインメントを要求していますが、これは、
・機械誤差要因を同時に推測する
・統計処理による誤差の圧縮
が目的だと思われます。
※ 角度の単位は断りのない限り「°(度)」で表記しています。
 |
| 戻る |