地平座標－赤道座標変換

経緯台は、「水平軸」と「高度軸」の２軸で構成される架台です。据付の安定性が高いので、大型の据付望遠鏡やドブソニアン型の移動望遠鏡でよく採用されています。近年では、市販の小型望遠鏡でも見受けられるようになってきました。
経緯台の欠点は、制御が赤道儀よりも格段にややこしいことです。

■「地平座標－赤道座標変換」について

経緯台の自動導入化のためには、以下の座標変換が必要となります。これは球面座標の計算には必ず出てくる事柄で、かつ基本的なものですが、私自身の整理のためにもここでまとめておきます。

○ [地平座標]→[赤道座標]変換: 望遠鏡の向き(方位，高度)の情報から赤道座標（赤経，赤緯）を得る変換。望遠鏡の向きを知るために必要。
○ [赤道座標]→[地平座標]変換: 赤道座標（赤経，赤緯）の情報から望遠鏡の向き(方位，高度)を得る変換。目的の星に向けるために必要。

恒星の位置は、図中の「赤経(α),赤緯(δ)」で与えられ、望遠鏡の向きは「方位(A),高度(h)」で示されます。実際には「赤経(α)」は図中に表れていませんが、これは「時角(t)」に変換され地平座標と仲介します。

■ 定義 ■
P ：天の北極
Z ：天頂
N ：真北
S ：対象星
φ：観測地の緯度
t ：恒星の時角
δ：恒星の赤緯
A ：恒星の方位
h ：恒星の高度 (0≦h≦90)

(1) 時角(t)
「時角」とは、子午線と[天の北極－恒星] のなす角度です。ある観測地点である恒星の位置を示すために用いられる、天球上の変数のひとつです。言葉で書くと分かりにくいですが、要は（図１）の角度(t) です。「時角」とはいうものの、単位は「°」(角度の度)です。

時角(t)と恒星の赤経(α) には次の関係があります。
時角(t) = LST - α
ここで、(LST) は観測地のその瞬間の地方恒星時(Local Sidereal Time)で、これも単位は「°」(角度の度)です。

(2) [地平座標]→[赤道座標]変換
球面三角△ZPS において、球面三角の性質から、

cos(90-δ) = cos(90-h)・cos(90-φ)+sin(90-h)・sin(90-φ)・cos(180-A)　　--- (1)
sin(90-δ)・cost = sin(90-φ)・cos(90-h)-cos(90-φ)・sin(90-h)・cos(180-A)　　--- (2)
sin(90-δ)/sin(180-A) = sin(90-h)/sint　　--- (3)

上の式をそれぞれ変形して、(1)→(4)，(2)→(5)，(3)→(6) が得られる。

sinδ = sinh・sinφ-cosh・cosφ・cosA　　--- (4)
cosδ・cost = cosφ・sinh+sinφ・cosh・cosA　　--- (5)
cosδ・sint = cosh・sinA　　--- (6)
高度h の代わりに、天頂からの角度(天頂距離)z を用いることもありますが、この場合は、
sinδ = cosz・sinφ-sinz・cosφ・cosA　　--- (4)
cosδ・cost = cosφ・cosz+sinφ・sinz・cosA　　--- (5)
cosδ・sint = sinz・sinA　　--- (6) どちらを用いても構いません。

この(4)(5)(6)式により、地平座標(A,h) を赤道座標(t,δ) に変換する。

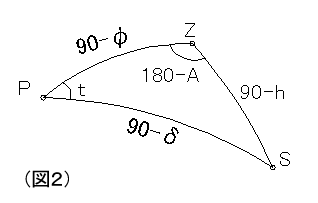
(3) [赤道座標]→[地平座標]変換
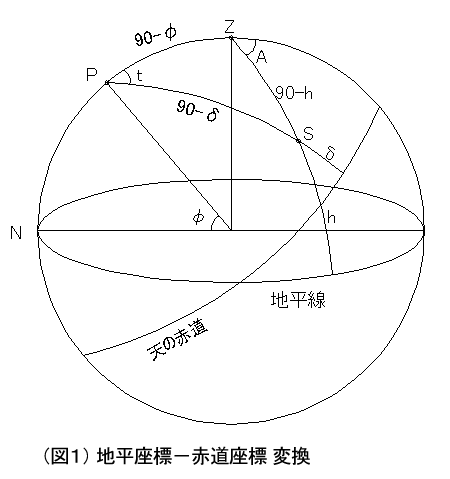
球面三角△PZS において、球面三角の性質から、

sin(90-h)/sint = sin(90-δ)/sin(180-A)　　--- (1)
sin(90-h)・cos(180-A) = sin(90-φ)・cos(90-δ)-cos(90-φ)・sin(90-δ)・cost　　--- (2)
cos(90-h) = cos(90-δ)・cos(90-φ)+sin(90-δ)・sin(90-φ)・cost　　--- (3)

上の式をそれぞれ変形して、(1)→(4)，(2)→(5)，(3)→(6) が得られる。

cosh・sinA = cosδ・sint　　--- (4)
cosh・cosA = -cosφ・sinδ+sinφ・cosδ・cost　　--- (5)
sinh = sinδ・sinφ+cosδ・cosφ・cost　--- (6)
高度h の代わりに、天頂からの角度(天頂距離)z を用いることもありますが、この場合は、
sinz・sinA = cosδ・sint　　--- (4)
sinz・cosA = -cosφ・sinδ+sinφ・cosδ・cost　　--- (5)
cosz = sinδ・sinφ+cosδ・cosφ・cost　--- (6)
どちらを用いても構いません。

この(4)(5)(6)式により、赤道座標(t,δ) を地平座標(A,h) に変換する。

■ 補足

さらに厳密には、以下の考慮が必要になりますが、これらはハードウエアから離れてプラネタリウムソフト側の問題となりますので項目のみを示します。詳しくは専門書をご覧下さい。

恒星の位置は「2000年分点」より「視位置」を
恒星の赤経赤緯は、地球の歳差により少しづつ移動しています。通常星表の位置は「2000年分点」で示されていますが、より精度の高い自動導入のために「視位置」で示される必要があります。
※ ここで言う「視位置」も厳密な表現ではなく「平均位置」か「歳差を考慮した位置」と呼ぶべきでしょうが、ソフトの表記では分かりやすく「視位置」と表現することが多いようです。恒星の固有運動までは考慮されない(不必要)ことが普通ですから、「歳差を考慮した位置」が一番正しい！
大気差補正

以上は赤道儀，経緯台ともに考慮すべきものです。

※ 角度の単位は断りのない限り「°(度)」で表記しています。

戻る