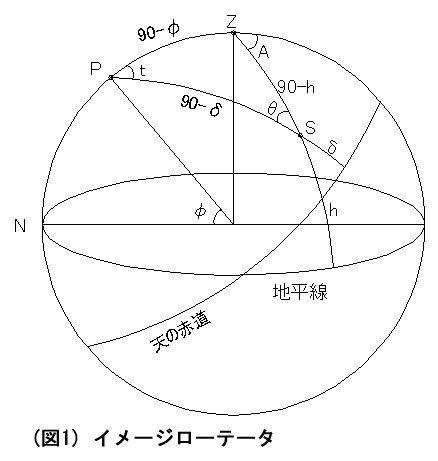
経緯台においては、視野は常に天頂方向に対して固定されます。一方、恒星は天の北極を中心として回転するので、
（図１）の恒星S に望遠鏡を向けた時、図のθが天頂方向を基準とした視野の回転角度となります。
このθが、時角ｔの変化に対する増加量 dθ/dt が求めたい「視野の回転スピード」です。
■ 「方位軸，高度軸の追尾速度」の計算式
経緯台においては、視野は常に天頂方向に対して固定されます。一方、恒星は天の北極を中心として回転するので、
（図１）の恒星S に望遠鏡を向けた時、図のθが天頂方向を基準とした視野の回転角度となります。
このθが、時角ｔの変化に対する増加量 dθ/dt が求めたい「視野の回転スピード」です。
■ 定義 ■
P ：天の北極
Z ：天頂
N ：真北
S ：対象星
φ：観測地の緯度
t ：恒星の時角
δ：恒星の赤緯
A ：恒星の方位
h ：恒星の高度 (0≦h≦90)
θ：視野の方位角
球面三角△ZPS において、球面三角の性質から、
sin(90-h)・sinθ = sin(90-φ)・sinｔ --------------(1)
sin(90-h)・cosθ = sin(90-δ)・cos(90-φ) - cos(90-δ)・sin(90-φ)・cosｔ ----------(2)
cos(90-h) = cos(90-φ)・cos(90-δ) + sin(90-φ)・sin(90-δ)・cosｔ -----------------(3)
この３式から、θ と h を求めます。h は(3)式から直ちに算出できます。
(1)/(2)より、
tanθ ＝ cosφ・sinｔ /(sinφ・cosδ - cosφ・sinδ・cosｔ) ----(4)
これで θ求まります。
θ(0≦θ＜360) の象限は、sinθの符号が(1)の符号に，cosθの符号が(2)の符号に一致することから判断します。
次に、dθ/dt を考えます。(1)(2)式の両辺を ｔ で微分すると、
-sinh・sinθ・dh/dt + cosh・cosθ・dθ/dt ＝ cosφ・cosｔ -----------(5)
-sinh・cosθ・dh/dt - cosh・sinθ・dθ/dt ＝ cosφ・sinδ・sinｔ ----(6)
この(5)(6)式から、dh/dt，dθ/dt について解くと、次の解が求められる。
dθ/dt ＝ (cosθ・cost - sinθ・sinδ・sint)・cosφ/cosh -----(7)
dh/dt ＝ -(sinθ・cost + cosθ・sinδ・sint)・cosφ/sinh ----(8)
以上で、dθ/dt は求められますが、右辺から θ と h を消すことも考えてみます。
球面三角△ZPS において、球面三角の性質から、
sin(180-A)・cos(90-h) ＝ sinθ・cost + cosθ・cos(90-δ)・sint
cos(180-A) ＝ -(cosθ・cost - sinθ・cos(90-δ)・sint)
変形して
sinA・sinh ＝ sinθ・cost + cosθ・sinδ・sint -----(9)
cosA ＝ cosθ・cost - sinθ・sinδ・sint ----------(10)
(7)式に(10)式を代入，(8)式に(9)式を代入して、
dθ/dt ＝ cosA・cosφ/cosh -----(11)
dh/dt ＝ -sinA・cosφ ---------(12)
さらに、球面三角△ZPS において、着目する頂点を移動して
sin(90-h)・cos(180-A) ＝ sin(90-φ)・cos(90-δ) - cos(90-φ)・sin(90-δ)・cost
変形して、
-cosh・cosA ＝ cosφ・sinδ- sinφ・cosδ・cost
これを cosA について解くと、
cosA ＝ (sinφ・cosδ・cost - cosφ・sinδ)/cosh
(11)式に代入して、
dθ/dt ＝ (sinφ・cosδ・cost - cosφ・sinδ)・cosφ/(cosh)^2 -----(13)
dθ/dt, dh/dt とも、赤道儀における恒星時駆動スピードの倍数で示されます。
以上で、イメージローテータに与える回転速度は計算できます。 しかしながら実機においては、「視野の回転中心」と「イメージローテータの回転中心」 を完璧に一致させないと意味がありません。 これは純粋に機械工作精度と調整の精度の問題で、イメージローテータを 導入するに当たっての最も高い障壁となることでしょう。
※ 角度の単位は断りのない限り「°(度)」で表記しています。
 |
| 戻る |