 2. 赤経軸と赤緯軸の直交誤差の自動導入に及ぼす影響(計算式)
2. 赤経軸と赤緯軸の直交誤差の自動導入に及ぼす影響(計算式)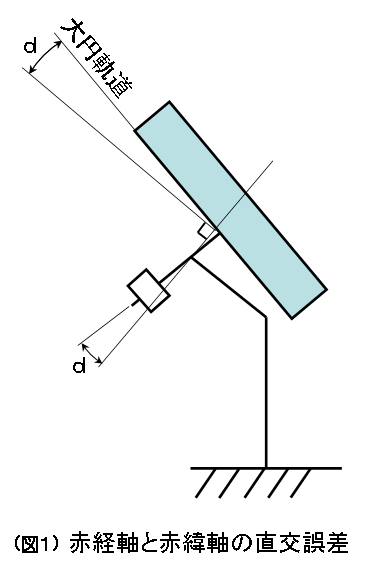 1. 「赤経軸と赤緯軸の直交誤差」とは
1. 「赤経軸と赤緯軸の直交誤差」とは「赤経軸と赤緯軸の直交誤差」とは、赤道儀の赤経軸と赤緯軸の工作誤差のことです。 自作の架台ならともかく、現代の赤道儀においてこの誤差は発生しにくく、発生してもその影響は小さいものでしょう。 誤差の要因としては重要ではありませんが、誤差要因としての影響を評価してみます。
この誤差は、望遠鏡の光軸と極軸の平行誤差によく似た傾向を示します。
しかし、直交精度は設計上当然のこととして製作されているのに対して、「光軸と極軸の平行誤差は調整すらされていない」
ことが通常です。複数の誤差要因を同時に修正することは困難(いじる必要のないところまでいじってしまうかも)なので、
まず、望遠鏡の光軸と極軸の平行誤差を対策し、それでも誤差が残る場合に赤道儀の赤経軸と赤緯軸の直交精度を
対策すべきでしょう。
 2. 赤経軸と赤緯軸の直交誤差の自動導入に及ぼす影響(計算式)
2. 赤経軸と赤緯軸の直交誤差の自動導入に及ぼす影響(計算式)
(1) この誤差の考え方
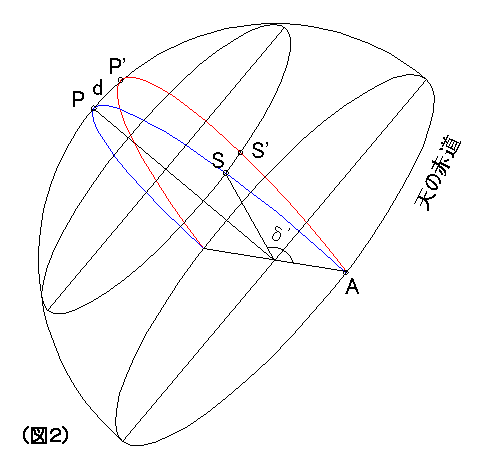
「赤経軸と赤緯軸の直交誤差」は、球面三角上では「大円が傾く誤差」として現れます。(図1)
(図2)は、(図1)の望遠鏡において、視野の向きが天球上をどのように辿るかを示した球面図です。
■ 定義 ■この ⊿α,⊿δ が 自動導入において赤経軸と赤緯軸の直交誤差の及ぼす影響となります。
d: 赤経軸と赤緯軸の直交誤差
# 赤道上の 点A でアライメントし赤緯軸を回転して 点S' に望遠鏡を向ける。
# 直交誤差が0であれば、視野は 天の北極P の方向を目指すはずであるが、
# 誤差があるためそうはなっていない。このとき、
δ : S' に向けた時の赤緯目盛
δ' : S' の真の赤緯
⊿α: 赤経の導入誤差(∠SPS')
⊿δ: 赤緯の導入誤差(δ'-δ)
とする
 (2) 自動導入において赤経軸と赤緯軸の直交誤差の及ぼす影響の計算
(2) 自動導入において赤経軸と赤緯軸の直交誤差の及ぼす影響の計算
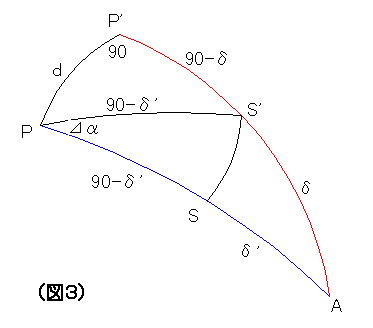
(図3)は、(図2)の一部を抜き取ったものです。
PA = P'A = 90°
球面三角△PP'S' より、∠P'=90°だから
cos(90-δ') = cosd・cos(90-δ)
sinδ' = cosd・sinδ
よって
⊿δ= δ'- δ = arcsin(cosd・sinδ) - δ ---- (1)
ここで、誤差dを微小とすると、
⊿δ= δ'- δ ≒ 0 となります
つまり、この誤差dが赤緯に与える影響はほとんどありません。
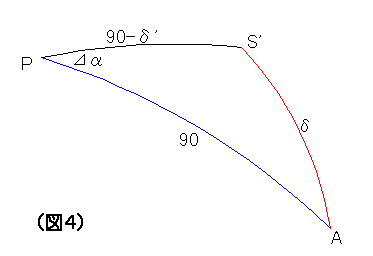 球面三角△PS'A から ∠APS'= ⊿α を求める
球面三角△PS'A から ∠APS'= ⊿α を求める
cosδ = cos(90-δ')・cos90 + sin(90-δ')・sin90・cos(⊿α)
これを変形していく
cosδ = cosδ'・cos(⊿α)
cos(⊿α) = cosδ/cosδ'
よって、
⊿α = arccos(cosδ / cosδ') ---- (2)
この式(2)は厳密な解ですが、近似的に、
⊿α = d・tanδ
と表すことができます。どちらを採用しても大差ありません。
この式が意味するところは、赤緯δが高くなると、加速度的に赤経方向の誤差 ⊿α が拡大されるということです。
赤経の目盛りは、高緯度になるにつれて狭くなるので、誤差が拡大される効果があるのです。
(3) 実際の誤差の現れ方
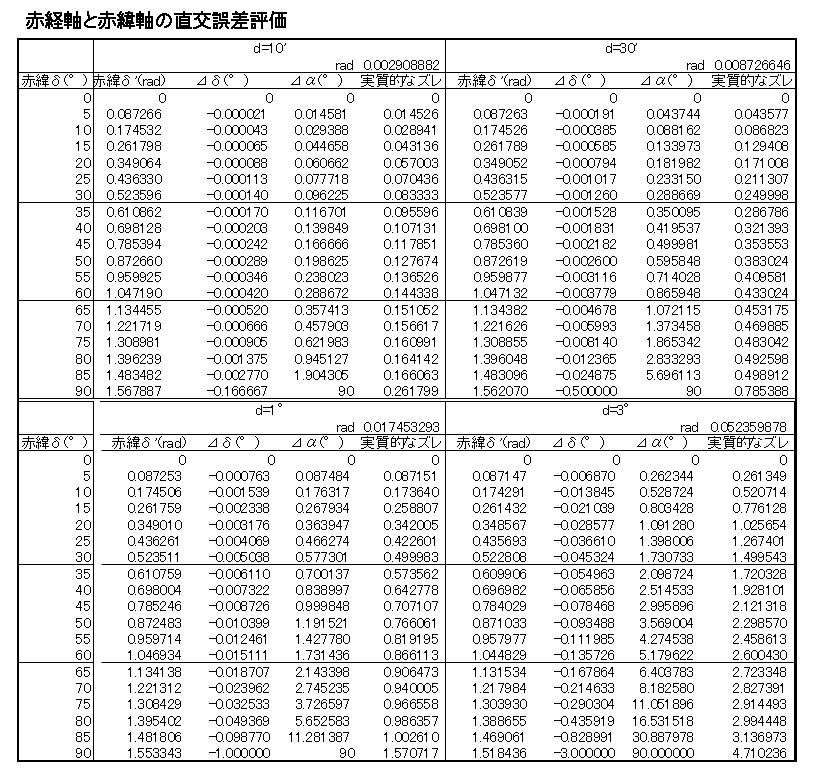
下表は 式(1),式(2) に基づき、光軸と極軸の誤差 d が及ぼす 誤差 ⊿α,⊿δ を計算したものです。
「実質的な誤差」とは、赤経目盛りが赤緯が高くなると狭くなる効果を排除した数値「⊿α・cosδ」です。
実質的な誤差は、高赤緯でもそれほど大きなものにはなりませんが、赤経目盛りが狭くなるため自動導入時の赤経方向の誤差 ⊿α
が拡大されることがわかります。
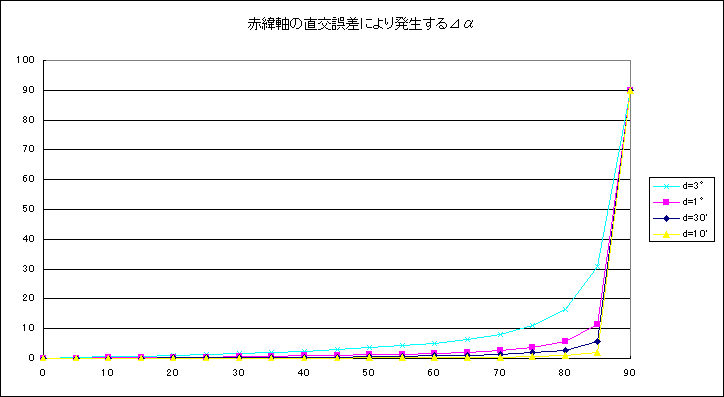
下図は上表の⊿αをグラフ化したものです。望遠鏡の光軸と極軸の平行誤差が及ぼす影響に
よく似た傾向を示すことが分かります。このことは、⊿αの実測によって両者を区別することは困難(区別がつかない)
ということでもあります。
数値そのものは、同じdに対して「赤道儀の赤経軸と赤緯軸の直交精度」が「光軸と極軸の誤差」
よりも常に大きな値を示します。しかしながら、「赤道儀の赤経軸と赤緯軸の直交精度」は意識されて設計製造されているのに対し、
「光軸と極軸の誤差」は通常は考慮されていないため、事実上後者が誤差の大半を占めています。
横軸:赤緯(°) / 縦軸:誤差⊿α(°)
※ 角度の単位は断りのない限り「°(度)」で表記しています。
 |
| 戻る |