
仭 掕媊 仭偙偺 嚈兛,嚈兟 偑 帺摦摫擖偵偍偄偰愒宱幉偲愒堒幉偺嬌幉僙僢僩岆嵎偺媦傏偡塭嬁偲側傝傑偡丅
# 嬌幉偑惓偟偔僙僢僩偝傟偰偄側偄朷墦嬀傪慜採偲偡傞丅
# 揤偺愒摴偲巕屵慄偺岎揰So 偱傾儔僀儞儊儞僩偟丄揰S 偵朷墦嬀傪岦偗傞丅
# 偙偺偲偒丄恀偺嵗昗偲朷墦嬀偺栚惙娐偲偺岆嵎乮嚈兛丆嚈兟乯傪媮傔傞丅
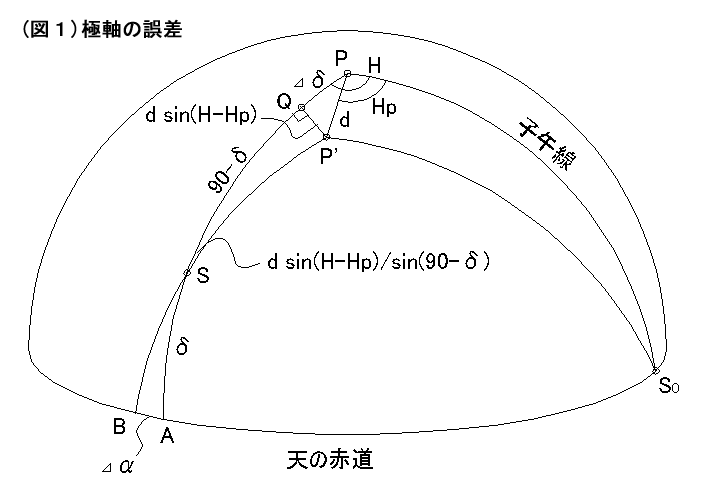
P 丗揤偺杒嬌
P'丗朷墦嬀偺嬌幉
d 丗嬌幉偺僙僢僩岆嵎丅棧妏
Hp丗嬌幉偺僙僢僩岆嵎丅帪妏
So丗巕屵慄偲揤偺愒摴偺岎揰丅婎弨偵掕媊
S 丗朷墦嬀偺岦偄偨曽岦
H 丗朷墦嬀偺岦偒偺帪妏
兟丗朷墦嬀偺岦偒偺愒堒
嚈兛丗 愒宱偺摫擖岆嵎
嚈兟丗 愒堒偺摫擖岆嵎
偲偡傞
乮恾侾乯偵偍偄偰丄俽俹亖90亱- 兟丆俽俹乫亖90亱- 兟乫
乮兟偑揤懱偺愒堒丆兟乫偑朷墦嬀偺栚惙娐偑帵偡愒堒乯偩偐傜丆乮恾侾乯偐傜
丂丂嚈兟 亖 兟乫- 兟 亖 d丒cos(H - Hp) 丂------ (1)
偲側傝傑偡丅乮d 傪彫偝偄偲偟偰 PP' 晅嬤傪暯柺偲傒側偟偰偄傞丅乯
丂帪妏偺曽偼彮偟岺晇偑偄傝傑偡丅
揤懱 S 偺帪妏 H 偼恾偺揤偺愒摴忋偺 ASo 偺挿偝偵摍偟偄偺偱丄H = ASo
堦曽丆揤偺杒嬌P 偲朷墦嬀偺嬌幉P' 偼偐側傝嬤偄偲偙傠偵偁傞偺偱丆帪妏傪峫偊傞偲偒偼
椉幰偺戝墌乮揤偺愒摴乯偼摨偠傕偺偲尒橍偣傑偡丅偦偆偡傞偲丆朷墦嬀偵懳偡傞帪妏偼 BSo 偺挿偝偱偡丅
傛偭偰帪妏曽岦偺曗惓検嚈兛 偲偄偆偺偼乮恾侾乯偺 AB 偺挿偝偵側傝傑偡丅
偙傟傪媮傔傞偨傔偵丆傑偢 [d丒sin (H - Hp)] 偲彂偄偨屖偺挿偝偐傜
丂佢PSP' 亖 d丒sin(H - Hp) / sin(90亱- 兟)
偵側傞偙偲偑傢偐傝傑偡乮P' 偐傜戝墌 SP 偵壓傠偟偨悅慄 P'Q 傪 S 傪嬌偲偡傞彫墌偺堦晹偲傕尒橍偟偰偄傑偡乯
sin (90亱- 兟) 偼傛傝惓妋偵偼 sin (90亱- 兟 - d cos(H -Hp)) 偲偡傋偒偱偡偑丆d 偑彫偝偄偱偡偐傜丆
寢壥傪 d 偺1師傑偱偵偡傞偙偲偵偡傟偽丆偙偺晹暘偼柍帇偱偒傑偡丅
嚈兛 偼偙傟偵 sin 兟 傪偐偗傟偽媮傔傜傟傑偡乮偙偙偱傕俙俛傪俽傪嬌偲偡傞彫墌偺堦晹偲尒橍偟偰偄傑偡乯丅
廬偭偰丄
丂丂嚈兛 亖 d丒sin(俫-俫p)丒tan兟 丂------ (2)
偑摫偐傟傑偡丅
偙偺 (1)(2)幃偑丄嬌幉偺偢傟偨朷墦嬀偵傛傞帺摦摫擖帪偺岆嵎偱偡丅
俀丏嬌幉岆嵎偺塭嬁
(1) 愒堒曽岦偺曗惓検
慜崁偺(1)幃
丂丂嚈兟 亖 d丒cos(H - Hp) 丂------ (1)
傛傝丄 -d 亝 嚈兟 亝 d 偲側傞丅
偮傑傝丄愒堒曽岦偺岆嵎(嚈兟)偼嬌幉偺岆嵎(d)傪挻偊側偄偙偲偐傜丄
偁傑傝恄宱幙偵峫偊傞昁梫偼側偄丅
偙偺岆嵎偑嵟戝抣偲側傞偺偼丄H = Hp 偲 H = -Hp 偺帪丄偡側偼偪丄揤懱S丆揤偺杒嬌P丆朷墦嬀偺嬌P' 偑
堦捈慄忋偵暲傇帪偱偡丅
(2) 帪妏曽岦偺曗惓検
慜崁偺(2)幃
丂丂嚈兛 亖 d丒sin(俫-俫p)丒tan兟 丂------ (2)
偙偺幃偑堄枴偡傞偲偙傠偼丄愒堒兟偑崅偔側傞偲丄壛懍搙揑偵愒宱曽岦偺岆嵎 嚈兛 偑奼戝偝傟傞偲偄偆偙偲偱偡丅
愒宱偺栚惙傝偼丄崅堒搙偵側傞偵偮傟偰嫹偔側傞偺偱丄岆嵎偑奼戝偝傟傞岠壥偑偁傞偺偱偡丅
懠偺岆嵎梫場丄愒宱幉偲愒堒幉偺捈岎岆嵎偵傛傞愒宱偺摫擖岆嵎 嚈兛 = d丒tan兟 偲斾妑偡傞偲丄
摨偠 d 偵懳偟偰偼丄sin(俫-俫p) 偑妡偐偭偰偄傞偨傔偵丄嬌幉偺岆嵎偼捈岎岆嵎傛傝傕岆嵎偺塭嬁偑彫偝偄偲偄偆偙偲偑傢偐傝傑偡丅
偙偺岆嵎偑嵟戝抣偲側傞偺偼丄(H - Hp) = 90亱偺帪丄偡側偼偪丄揤懱S 偺埵抲偑
揤偺杒嬌P亅朷墦嬀偺嬌P' 偺尫偵懳偟偰捈妏曽朄偵偁傞偲偒偱偡丅
嬌幉偺岆嵎偼偳偺朷墦嬀偱傕挷惍曽朄梡堄偝傟偰偍傝丄娤應幰偺堄幆傕崅偄偨傔丄尰幚揑側朷墦嬀偺岆嵎梫場 偲偟偰彫偝偄傕偺偲峫偊傜傟傑偡丅
 仭 掕媊 仭
仭 掕媊 仭
# 嬌幉偑惓偟偔僙僢僩偝傟偰偄側偄朷墦嬀傪慜採偲偡傞丅
# 揤偺愒摴偲巕屵慄偺岎揰So 偱傾儔僀儞儊儞僩偟丄揰S 偵朷墦嬀傪岦偗傞丅
# 偙偺偲偒丄恀偺嵗昗偲朷墦嬀偺栚惙娐偲偺岆嵎乮嚈兛丆嚈兟乯傪媮傔傞丅
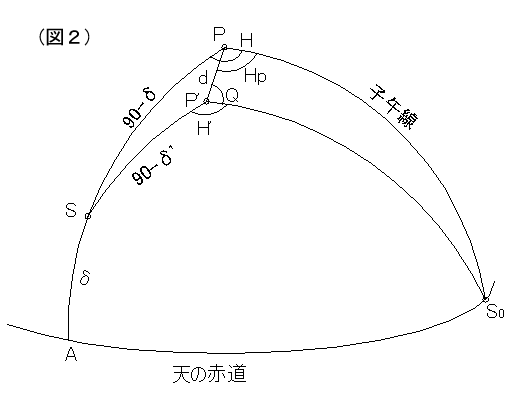
P 丗揤偺杒嬌
P'丗朷墦嬀偺嬌幉
d 丗嬌幉偺僙僢僩岆嵎丅棧妏
Hp丗嬌幉偺僙僢僩岆嵎丅帪妏
So丗巕屵慄偲揤偺愒摴偺岎揰丅婎弨偵掕媊
S 丗朷墦嬀偺岦偄偨曽岦
H 丗朷墦嬀偺岦偒偺恀偺帪妏
兟丗朷墦嬀偺岦偒偺恀偺愒堒
H'丗朷墦嬀栚惙偺帪妏
兟'丗朷墦嬀栚惙偺愒堒
偲偡傞丅
嚈兛乮愒宱偺摫擖岆嵎乯亖 H' - H
嚈兟乮愒堒偺摫擖岆嵎乯亖 兟'- 兟
偱偁傞偐傜丄H', 兟'傪婛抦偲偟偨偲偒偺 H, 兟傪媮傔傞
傑偢丄尫P'So 偲 佢Q(=佢PP'So 偲掕媊) 傪媮傔傞丅
仮PP'So 偵偮偄偰丄媴柺嶰妏偺岞幃偐傜丄
丂sinP'So丒sinQ 亖 sin90丒sinHp ----------- (1)
丂sinP'So丒cosQ 亖 sind丒cos90 - cosd丒sin90丒cosHp --- (2)
丂cosP'So 亖 cosd丒cos90 + sind丒sin90丒cosHp ---------- (3)
(3) 傛傝丄P'So 傪媮傔傞丅徾尷偼丄 90-d 亝 P'So 亝 90+d (d偼彫偝偄)
偺斖埻偱敾抐偡傞丅
(1)/(2) 偵傛傝丄
丂tanQ 亖 -tanHp / cosd ----------------- (4)
徾尷偼丄(1)(2)幃偐傜P'So 偺夝偲塃曈偺晞崋偱敾抐偡傞丅埲壓丄徾尷偺寛傔曽偼摨條丅
埲忋丄(4)傛傝丄佢Q 偑寛傑傞丅偙偺 佢Q 傪拠夘偟偰 兟 偲 H 傪媮傔傞丅
偙偙偱丄朷墦嬀偺嬌幉偐傜朷墦嬀偺岦偒偵帄傞尫P'S 偼丄P'S 亖 90 - 兟' 偵摍偟偄丅
仮PP'S 偵偮偄偰媴柺嶰妏偺岞幃偐傜丄
丂sin(90-兟)丒sin(H-Hp) 亖 sin(360-Q-H')丒sin(90-兟') -------------------------- (5)
丂sin(90-兟)丒cos(H-Hp) 亖 sind丒cos(90-兟') - cosd丒sin(90-兟')丒cos(360-Q-H') --- (6)
丂cos(90-兟) 亖 cosd丒cos(90-兟') + sind丒sin(90-兟')丒cos(360-Q-H') -------------- (7)
(7)幃偐傜
丂sin兟 亖 cosd丒sin兟' + sind丒cos兟'丒cos(Q+H') ------------ (8)
兟偼丄(8)幃偐傜媮傔傜傟傞丅
(5)/(6) 偵傛傝
丂tan(H-Hp) 亖 -sin(Q+H')丒cos兟' /(sind丒sin兟' - cosd丒cos兟'丒cos(Q+H'))
偙偺幃偐傜 S 偺恀偺帪妏 H 偑媮傔傜傟傞丅
仸 妏搙偺扨埵偼抐傝偺側偄尷傝乽亱(搙)乿偱昞婰偟偰偄傑偡丅
 |
| 栠傞 |