 ■ 定義 ■
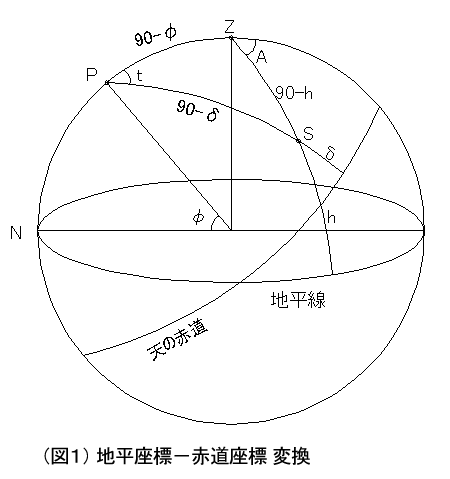
■ 定義 ■P :天の北極
Z :天頂
N :真北
S :対象星
φ:観測地の緯度
t :恒星の時角
δ:恒星の赤緯
A :恒星の方位
h :恒星の高度 (0≦h≦90)
1.経緯台の天頂問題
 ■ 定義 ■
■ 定義 ■
P :天の北極
Z :天頂
N :真北
S :対象星
φ:観測地の緯度
t :恒星の時角
δ:恒星の赤緯
A :恒星の方位
h :恒星の高度 (0≦h≦90)
方位軸,高度軸の追尾速度 の計算式より、
dh/dt = -sinA・cosφ --- (1) 高度方向の追尾速度
dA/dt = tanh・cosA・cosφ+sinφ --- (2) 方位方向の追尾速度
この式の意味するところを考察する。
(1) 高度軸の可変範囲
(1)式において右辺の、-1≦sinA≦1 , 0≦cosφ≦1 であるから、
-1 ≦ dh/dt ≦ 1
すなはち、
 高度軸の可変範囲は最大で恒星時スピードとなる
高度軸の可変範囲は最大で恒星時スピードとなる
(2) 方位軸の可変範囲 (天頂問題)
(2)式において右辺の、tanh により 高度h が90度に近くなると無限大になる。
sinφ≦ dA/dt ≦∞ (h=90度のとき ∞)
 方位軸は、天頂付近で極めて大きな追尾速度が必要となる
方位軸は、天頂付近で極めて大きな追尾速度が必要となる
以上が、天頂問題の数学的表現です。このため、経緯台式の架台においては、天頂を観測できないこと多く、
天頂からのある一定範囲を避けて制御しています。
2.「方位軸,高度軸の追尾速度」の実機への反映
前述の2式のうち、高度軸の回転速度は、-1 ≦ dh/dt ≦ 1 ですから特に問題になりません。 ここでは、方位軸の速度が実際にどの程度のスピードになるか、実際の数値を計算してみます。
○方位軸の追尾速度 dA/dt = tanh・cosA・cosφ+sinφ
(1) φ= 0°赤道上のとき
dA/dt = tanh・cosA
最大値は cosA=1 (南中時)
・h= 87°のとき :19.1
・h= 85°のとき :11.4
・h= 80°のとき : 5.7
(2) φ=30°のとき
dA/dt = 0.866 tanh・cosA + 0.5
最大値は cosA=1 (南中時)
・h= 87°のとき :17.0
・h= 85°のとき :10.4
・h= 80°のとき : 5.4
(3) φ=60°のとき
dA/dt = 0.5 tanh・cosA + 0.866
最大値は cosA=1 (南中時)
・h= 87°のとき :10.4
・h= 85°のとき : 6.6
・h= 80°のとき : 3.7
(4) φ=90°北極上のとき
dA/dt = 1 --- 恒星時に同じ
---- 以上より、「16倍速で設計」すれば、高度85°以下 で稼動可能となります。
もちろんこの数値の許容範囲を大きくする設計は可能ですが、これらの数値と天頂領域の制限
と天秤にかけることになります。
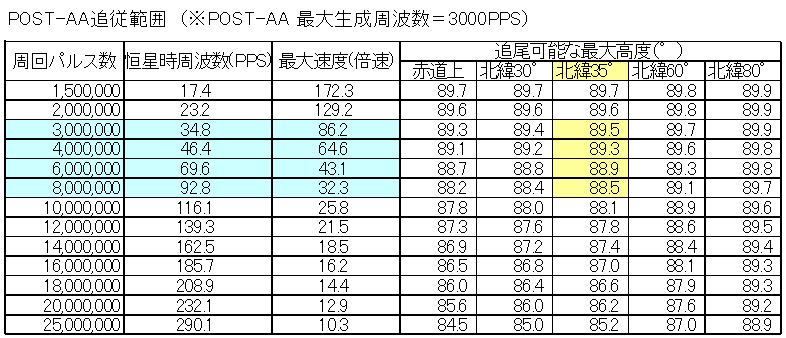
表中の 青の網掛け は機械部の現実的な範囲です。黄色の網掛け は、東京付近(北緯35°)で A-ZEUS を稼動できる範囲の目安となります。 このように東京付近では、高度88.5°以上のごく狭い範囲が天頂問題によって望遠鏡を向けられない領域となります。
天頂問題の及ぶ範囲は、機械系の周回パルス数と観測地の緯度によって異なるため、 瀬戸口貴司作による制御ソフト Yoc では、望遠鏡の向けられる範囲をソフト上で制限することができます。 デフォルトは高度85°と設定されています。
POST-AA は、Yoc からの1秒毎の通信により、追尾速度を修正しています。このため、本来の変速曲線を微視的には折れ線で近似
しており、本来の変速曲線との差は追尾誤差になります。
※ 角度の単位は断りのない限り「°(度)」で表記しています。
 |
| 戻る |