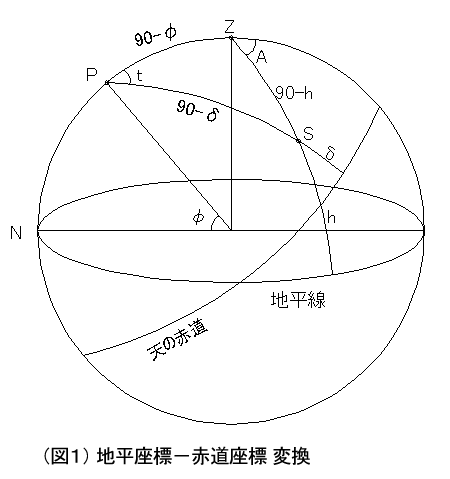
 ■ 定義 ■
■ 定義 ■P :天の北極
Z :天頂
N :真北
S :対象星
φ:観測地の緯度
t :恒星の時角
δ:恒星の赤緯
A :恒星の方位
h :恒星の高度 (0≦h≦90)
■ 「方位軸,高度軸の追尾速度」の計算式
 ■ 定義 ■
■ 定義 ■
P :天の北極
Z :天頂
N :真北
S :対象星
φ:観測地の緯度
t :恒星の時角
δ:恒星の赤緯
A :恒星の方位
h :恒星の高度 (0≦h≦90)
[赤道座標]→[地平座標]変換 の計算式より、
cosh・sinA = cosδ・sint --- (1)φ,δを定数として (3)式の両辺を t について微分
cosh・cosA = -cosφ・sinδ+sinφ・cosδ・cost --- (2)
sinh = sinδ・sinφ+cosδ・cosφ・cost --- (3)
cosh・dh/dt = -cosδ・cosφ・sint
よって、
dh/dt = -cosδ・cosφ・sint / cosh --- (4)
ここで、(1)式より
cosδ・sint / cosh = sinA
これを(4)式に代入して
dh/dt = -sinA・cosφ --- (5)
次に、φ,δを定数として (2)式の両辺を t について微分
-sinh・cosA・dh/dt-cosh・sinA・dA/dt = -sinφ・cosδ・sint
上式に(5)式を代入して
sinh・cosA・sinA・cosφ-cosh・sinA・dA/dt = -sinφ・cosδ・sint
変形して
sinh・cosA・cosφ-cosh・dA/dt = -sinφ・cosδ・sint / sinA
ここで、(1)式より
sinA = cosδ・sint / cosh
これを上式に代入して
sinh・cosA・cosφ-cosh・dA/dt = -sinφ・cosh
変形して
dA/dt = (sinh・cosA・cosφ+sinφ・cosh) / cosh
よって
dA/dt = tanh・cosA・cosφ+sinφ --- (6)
(5)(6)式が高度軸と方位軸の追尾速度となるdh/dt, dA/dt, dz/dt とも、赤道儀における恒星時駆動スピードの倍数で示されます。
dh/dt = -sinA・cosφ --- (5) 高度方向の追尾速度
dA/dt = tanh・cosA・cosφ+sinφ --- (6) 方位方向の追尾速度高度h の代わりに、天頂からの角度(天頂距離)z を用いることもありますが、この場合は、
dz/dt = sinA・cosφ --- (5) 高度方向の追尾速度
dA/dt = cosA・cosφ/tanz + sinφ --- (6) 方位方向の追尾速度
どちらを用いても構いません。
※ 角度の単位は断りのない限り「°(度)」で表記しています。
 |
| 戻る |